Probabilistic and stochastic approaches are often confused or used interchangeably, but they are two distinct concepts in probability theory. Both methods are used to infer or quantify the likelihood of outcomes, but each method does so in a different way. In this post, we’ll delve into the concepts of probabilistic and stochastic approaches, their similarities, differences, and how they can be applied in different contexts.
Probabilistic and stochastic models are both used to model uncertainty, but they take different approaches in doing so. Probabilistic models focus on estimating the probability of an event or outcome based on past data and probability distributions. One of the most common examples of probabilistic modeling is the use of regression models to predict an outcome based on a set of predictor variables that affect it. Probabilistic models use Bayesian inference, which involves updating probability distributions based on observed evidence.
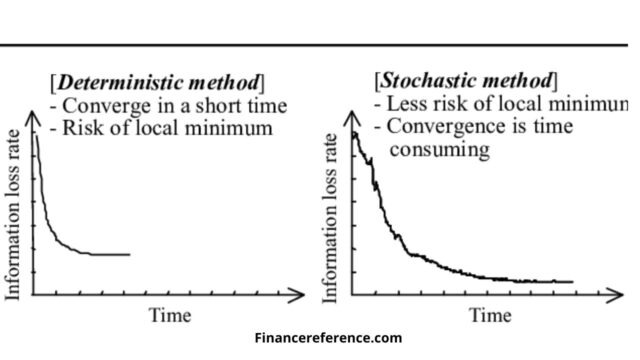
Stochastic models, on the other hand, focus on the randomness of an event or process. In stochastic modeling, variability is modeled as a random process using deterministic models or equations, and randomness is incorporated into the model. In other words, a stochastic model is a model that attempts to predict how a system or process will behave over time, taking into account the uncertainties and variability in the real-world data. Stochastic models are useful when probabilistic models may not be sufficient, such as in cases where the data is non-linear.
The main difference between probabilistic and stochastic methods is the way they deal with uncertainty. In probabilistic models, uncertainty is handled explicitly using probability distributions, while in stochastic models, it is accounted for implicitly through the use of randomness. With probabilistic models, you can quantify the probability of an event or outcome, which can be useful for making decisions with uncertain outcomes. With stochastic models, you can better understand how systems behave and evolve over time.
Both probabilistic and stochastic approaches have their strengths and weaknesses, depending on the problem or task at hand. Probabilistic methods are useful when there is ample historical data that can be used to estimate the probability distribution of an event or output. Additionally, these methods give decision-makers a range of outcomes, which can be useful when trying to understand risk or manage uncertainty. Stochastic methods, on the other hand, can model the dynamics of complex systems with many variables, where the relationships between them are not well understood.
In conclusion, it is important to understand the difference between probabilistic and stochastic modeling because they both have their strengths and weaknesses, depending on the problem at hand. Probabilistic models are well-suited for cases where historical data can be used to estimate the probability of an event or output. Stochastic models are useful when trying to model the dynamics of complex systems with many variables where the relationships between them are not well understood.
In practice, the choice between probabilistic and stochastic methods depends on the specific problem at hand, including the available data, the level of uncertainty, and the types of outcomes or outputs being modeled. Both probabilistic and stochastic methods can help in making better decisions by quantifying uncertainty and predicting outcomes.